What is the right lens and resolution for your IP camera? When you put together your IP camera system, you want to make sure that the camera you select for each location meets your expectations. It is important to first know the objectives for each area you are viewing. Do you want to identify a person’s face, a license plate, or just detect a person walking far away? In general, the more detail you want, the higher the resolution you need. This article shows you how to determine the viewing area and distance you should expect.

Note: this article was updated on 8/15/2017 to correct an error in calculation.
First understand that the number of pixels per ft. (or per m) determines the detail we can see. The higher the resolution of the IP camera, the wider the area we can see at a specific pixel/ft. When there are enough pixels covering a person’s face, we can recognize the person. The lens allows us to frame our field of view. We can select a lens that allows us to see an area 10 ft. (3 m) away or a different lens that magnifies an area that’s over 10,000 ft. (3048 m) away.
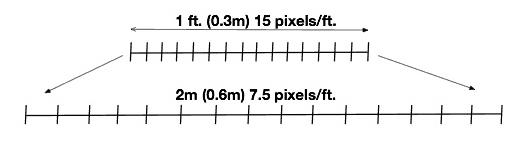
The lens controls how wide our field of view will be. The wider our field of view the less pixels per ft (or meter) we will get. Let’s look at a simple example. Take a look at the line below. The line is broken into small sections or horizontal pixels. The more elements per distance (pixels/m or pixels/ft.), the more detail we can see. As we adjust our lens to provide a wider view, the number of pixels/ft. (m) decreases and the less detail we can see.
Determining the Viewing Area or Field of View.
In a previous article, we discussed the resolution required to identify a person’s face. We determined that if there is good light you will require about 80 horizontal pixels/ft. (260 pixels/m) to identify someone you know. But, if you need to identify a person you don’t know then you need a lot more resolution. It requires about 150 pixels/ft. (492 pixels/m). We consider this higher pixel count to be more of a forensic identification than a personal identification.
Calculating the field of view:
How wide a field of view can we see and still be able to identify a person’s face? To calculate the widest field of view, divide the number of horizontal pixels (available from the camera) by the pixels/ft. you would like to achieve. The following formula is used to determine the field of view:
Total Horizontal Resolution / Pixels per ft. = Field of View
For the following example, let’s assume you would like to identify the face of a person you already know. If the camera resolution is 1920 x 1080 pixels (2-megapixel), then our widest field of view is:
1920/80 = 24 ft. (7.3 m).
If we have a 5-megapixel camera with a resolution of 2592 x 1944, then the widest horizontal field of view is 32.4 ft. (9.9 m). And, a 10-megapixel camera, with 3648 x 2752 pixel resolution, provides a 45.6 ft. (14 m) field of view.
We can also do this calculation in reverse. We can start with the field of view and then calculate the resolution of the camera. Use the following formula to calculate the resolution of the IP camera:
(Field of View) x (pixels/ft.) = Horizontal Resolution
If we want a field of view of 20 ft. and we need 80 pixels/ft. then the formula indicates:
20 ft. x 80 pixels/ft. = 1600 pixels (horizontal)
We can now select a camera that has at least 1600 horizontal pixels. For example, the Sony SNC-EM630 IP camera has a resolution of 1920 x 1080 pixels. This is a very nice 2.0 mega-pixel camera with enough resolution to meet these requirements. It is also one of the newer IP camera models that provides excellent low light sensitivity and wide dynamic range (WDR).
Calculating Distance based on the Camera Lens Angle
Someone once asked, how far away can I see with my IP camera? Well, you can see pretty far away. You can view the moon which is 238,900 miles (384,400 km) away. Of course you can’t see too much detail at that distance.
So how do you calculate the distance based on the detail you want to see. Well, there are a number of ways to do it. There are some calculators available from various manufacturers, but they tend to use the F-number of the lens (mm) rather than the lens angle or are very specific to the manufacturer’s cameras. The best way to measure the distance is to use trigonometry. Hopefully, you didn’t sleep through that class in school (like I did). We start with the angle of the lens mounted on specific cameras. The lens plus the sensor size determines the actual angle so we rely on the angles provided by the camera manufacturer or the lens manufacturer.
We can use the segment of a circle or a right-triangle calculator to calculate the distance from the camera. The circle segment is more accurate, but the triangle method is easier because we can use a right-triangle calculator.
Using the triangle to calculate the distance when we have a 30-degree lens
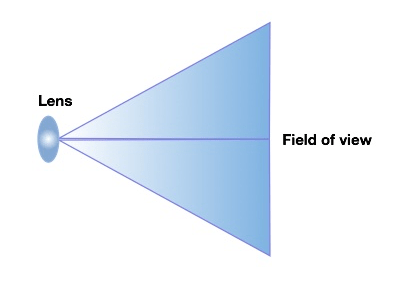
Let’s use a 2-megapixel camera in this example. The resolution of the camera sensor is typically 1920 (H) x 1080 (V) pixels. Let’s assume we want to identify someone we know, so we need 80 pixels per ft. to do this.
Step one is to draw a triangle with the peak of the triangle at the lens and the base at the field of view. To make the calculations split the triangle into two right triangles.
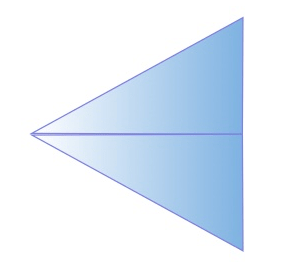
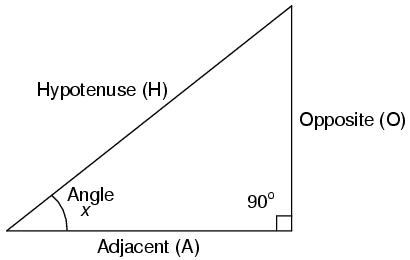
We will use the right-triangle calculator to calculate the distance to the viewing area. For example, there’s a calculator located at http://www.cleavebooks.co.uk/scol/calrtri.htm, and another at http://www.mathportal.org/calculators/plane-geometry-calculators/right-triangle-calculator.php
As I mentioned, the 2-megapixel camera provides a maximum width of 24 ft (7.3 m). Since we cut the triangle in half, the opposite side (O) is equal to 12 ft (3.7 m).
Suppose the camera we select has a variable lens, and we decide to set the lens at 30-degrees, cut that in half and Angle x equals 15- degrees. Using the right-angle triangle calculator, we find that the hypotenuse side (H) is 46 ft. (14 m) away from the camera lens.
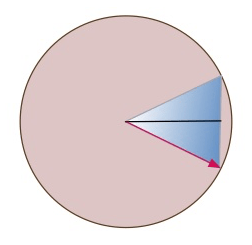
Using the Segment of a Circle
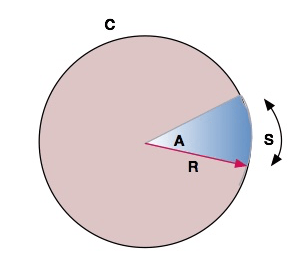
Calculating the distance using a segment of a circle requires a different formula.
C= circumference
S= segment of the circumference
A= angle of the lens
R = distance (or radius of the circle)
To calculate the radius (distance) using the segment method, we use the formula C=2πr.
Since a 30-degree segment of the circle is 1/12 of 360-degrees we need to calculate the circumference using the following formula:
C= S x 360/A
In this case C= 24 ft. x 360/30 = 24 x 12 = 288 ft. (87.8 m)
Now we have the circumference, we can calculate the radius:
C/(2π) = R
288/(2 x 3.14) = 45.9 ft. (14 m)
As you can see, both methods provide similar answers, but as the angle increases the segment method is more accurate. The difference between the arc and the chord of the circle become greater as the angle increases. When the angle approaches 180 degrees the triangle method doesn’t work.
Calculating the Distance Using a Panoramic Lens
Note: this section of the article was updated on 8/15/2017 to correct an error in calculation.
How far can you be from a panoramic 360-degree camera and still be able to identify a person’s face? The triangle calculation won’t work, so we must use the circle calculation for this.
First we must make sure we have enough resolution in the total circumference. In the example above we were only looking at one segment of the circle (1/12th of the circumference, or 30-degrees), but in this example, we are looking at the 180-degree view provided by the panoramic camera. This is equal to 1/2 the circumference (or 180 degrees).
So let’s start the calculations again. As mentioned before, we need 80 pixels/ft. The 2-megapixel camera, provides a resolution of 1920 x 1080 pixels. When calculating the field of view for a panoramic lens, we use the vertical resolution rather than the horizontal resolution. This is because the filed of view is square rather than rectangular. The field of view required to identify a person’s face in a linear field of view is 1080/80 = 13.5 ft. This is half the total circumference. Since the segment covers 1/2 the circle the circumference is 2 x 13.5 ft = 27 ft. Again we use the formula to calculate the radius (which is the distance from the camera):
C/(2π) = R
27/(2 x π) = 4.3 ft. (1.3 m)
If you want to recognize people further away, you would need a lot more resolution. The higher the resolution, the more pixels are in the circumference (field of view), and consequently the further away we can see the same detail. As an example, a 12-megapixel camera, provides a maximum 37.5 ft. (11.4 m) FOV. It provides enough resolution to identify a person’s face 11.9 ft. (3.6 m) away from the camera.
Summary
We first determine what we want to see, and then we can calculate the IP camera resolution and lens to use. Once we know how much resolution we need, we can calculate the size of the field of view and distance from the camera, based on the lens we select. To get a rough idea of how far away we can see a certain amount of detail, we can use the right-triangle calculator, but when our angles get very large it is better to use the circle calculation.
If you need help with these calculations, don’t hesitate to give us a call. We have a lot of experience with IP camera systems and can help you get the exact surveillance system you need. Contact us at 914-944-3425 or 1-800-531-1658 (in the USA), or just use our contact form.